1A.  CONJUNCTIONS.

The following are some of the more common conjunctions:

1B.  Kai (και)

This is by far the most common conjunction, and is most often translated "and" (connecting two words or phrases or sentences together).

Consider its significance in 1 Timothy 3:16--"And..."  Most commentators see no vital connection between the church described in verse 15 and "the mystery of godliness" described in verse 16, but the use of και proves that the two verses were tied together in the mind of the Apostle.

This conjunction can also be translated "also" or "even" as well as in other ways that reflect less common usages.  But it is most commonly translated "and."

2B.  hina (ινα)

Most commonly this conjunction is used to denote PURPOSE, and often can be translated "that" or "in order that."  See Matthew 7:1 and 2 Corinthians 5:15.

3B.  gar  (γαρ)

This conjunction is most frequently used to give a reason or an explanation for what has just been said (see Matthew 1:21).  The Apostle Paul used this conjunction again and again (see Romans 10:2,3,4,5,10,11,12,13, etc.).  Thus, this word explains the preceding context.

4B.  oun   (ουν) 

This conjunction is most often inferential and can often be translated "therefore, consequently."  The writer is making an inference or a conclusion in light of what he has just written.  Here are some examples:  Ephesians 4:1 (a conclusion based on the first three chapters); Romans 12:1 (a conclusion based on the first 11 chapters); James 4:4 (a conclusion based on the first half of the verse); Romans 3:28 (Paul's conclusion based on his careful argument here in chapter 3).  Hence, when you find this conjunction, it should force you to study the preceding context.  Other  inferential conjunctions are απα  (which introduces a conclusive statement), and  διο (which is the strongest inferential conjunction).

5B.  alla  (αλλα) 

This is a strong adversative conjunction (it was one of the strongest ways the Greeks could say, "BUT").  It often expresses a strong contrast.  See Matthew 4:4; 2 Corinthians 4:8 and Titus 3:5.  It can be translated in some contexts as "yet, rather, nevertheless, certainly, etc."  But most often it is translated, "but."

6B.  de   (δε)

This is another adversative conjunction, perhaps somewhat milder than  αλλα, but also meaning "but, however, yet, on the other hand."  See Romans 6:23; Ephesians 2:4; Titus 3:4.  However, this word is also used without the adversative meaning and can simply be translated "and" or "now," etc.

7B.  hoti    (οτι)

This conjunction is commonly used as a causal particle meaning "because" or "for."  In this sense it occurs in each one of the beatitudes (Matthew 5:3ff).  It thus answers the question "WHY?".   Why are the poor in spirit happy?  Because the kingdom belongs to them!

2A.  PREPOSITIONS.

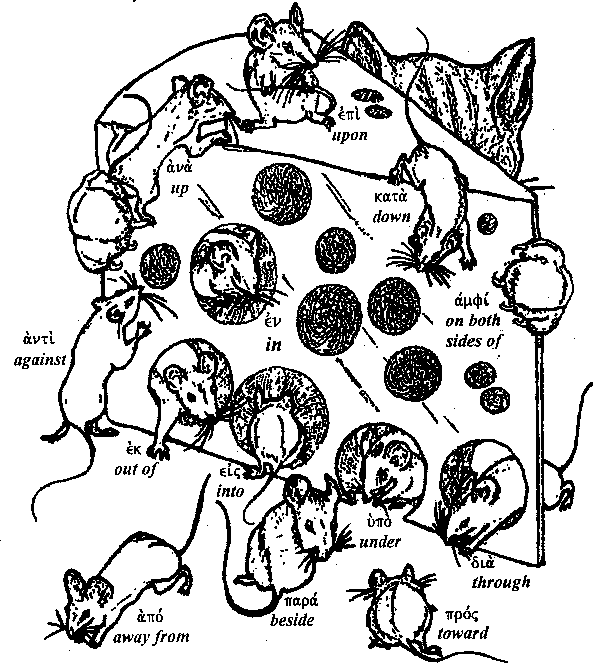
The following chart (adapted from A Manual Grammar of the Greek New Testament by Dana and Mantey, p. 113) may help you to understand the basic local and spiritual significance of the common Greek prepositions:

Caution:  These pronouns do not always have the spatial meanings as shown above. For example,  κατα often means "according to" and υπο often means "by" (he was baptized by John) and δια often means "because of" and υπερ often means "for, on behalf of" (Christ died for our sins--1 Cor. 15:3), etc.

The following is another illustration of how the Greek prepositions relate spatially. Follow the mouse trail!

Greek Prepositions

*     *     *     *     *     *

You have now finished our study of  Englishman's Greek.  Beware lest  you think that your knowledge of Greek and of grammar will in and of itself help you to know God and His Word better.  Our Lord did not say, "If any man becomes proficient in Greek, he shall know of the doctrine" (John 7:17).  No, He said, if any man desires to do His will, he shall know..."  Why should God reveal His will and His Words to someone who is not willing to follow or obey?  Beware!  Sad to say, many Greek scholars have been heretics, and many people who had no knowledge of Greek have lived godly in Christ Jesus. A knowledge of Greek can be a helpful tool in understanding the Scriptures, but the key is a right and healthy relationship with the living Christ.